
출처: https://www.acmicpc.net/problem/1654
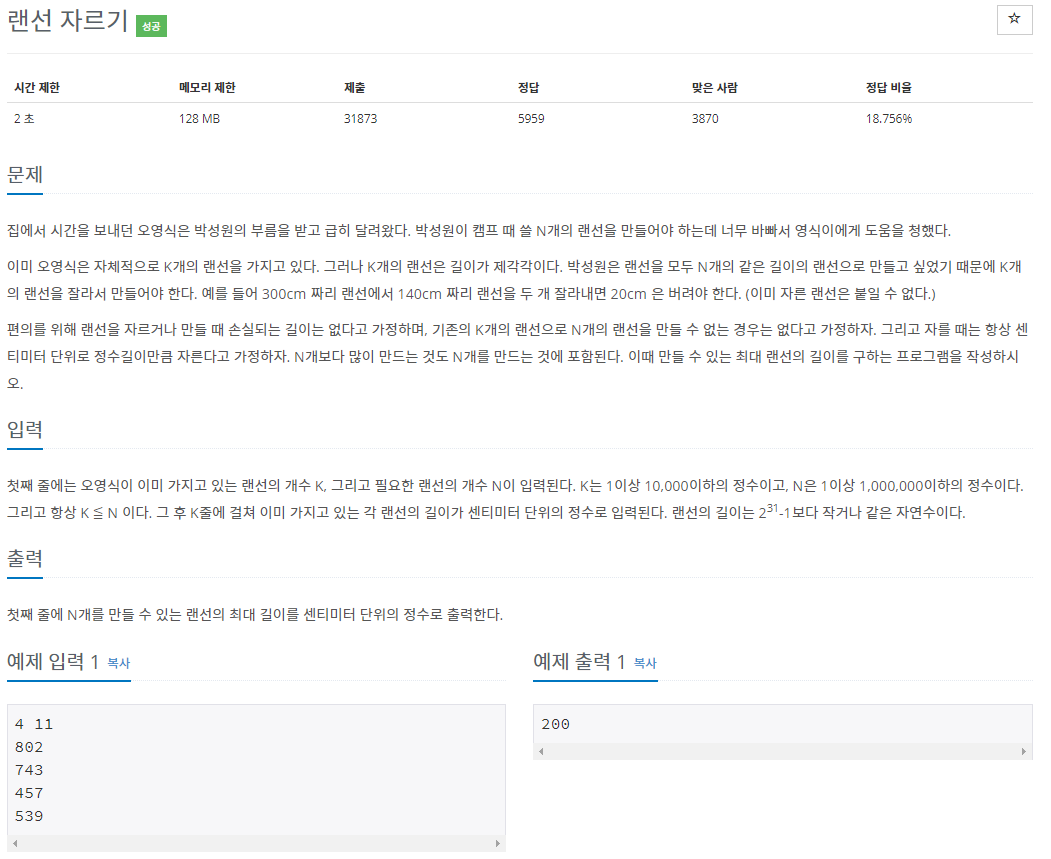
1654번: 랜선 자르기
첫째 줄에는 오영식이 이미 가지고 있는 랜선의 개수 K, 그리고 필요한 랜선의 개수 N이 입력된다. K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수이다. 그리고 항상 K ≦ N 이다. 그 후 K줄에 걸쳐 이미 가지고 있는 각 랜선의 길이가 센티미터 단위의 정수로 입력된다. 랜선의 길이는 231-1보다 작거나 같은 자연수이다.
www.acmicpc.net
이분 탐색을 사용하면 쉽게 풀 수 있는 문제이다.
이분 탐색의 대표적인 예제인 "나무 자르기" 같은 문제를 풀었다면, 약간의 변화만 줘도 이 문제를 맞힐 수 있을 것이다.
풀이
이진 검색 알고리즘 이라고도 불리는 이분 탐색 알고리즘은 O(logN)의 시간 복잡도를 갖는 탐색 알고리즘의 종류 중 한 가지이다.
먼저 문제를 풀기 위해 뼈대가 되는 코드를 작성했다.
if __name__ == "__main__":
K, N = map(int,input().split())
arr = []
for _ in range(K):
arr.append(int(input()))
arr.sort(reverse = True)
print(solution(K, N, arr))입력을 받으면서 리스트 arr에 원소를 하나씩 추가해주는 과정이 있다.
리스트를 정렬 후 함수의 매개변수로 넘겨주는 이유는 아래 코드를 보면 알 수 있다.
def solution(k,n, arr):
high = arr[0]
low = 0
result = 0
while low <= high:
mid = (high + low) // 2
cnt = 0
if mid == 0: return 1
for val in arr:
cnt += val//mid
if cnt >= n and mid > result:
result = mid
break
if cnt < n:
high = mid - 1
else:
low = mid + 1
return result1. low, result 변수에 각 각 0을 대입하고, high에는 arr[0]을 대입한다.
* 이 부분이 내가 리스트를 정렬해서 넘겨준 첫 번째 이유이다. 파이썬에서 제공하는 max함수가 조금 더 빠르지만, 이후 반복문에서 정렬된 리스트가 시간 효율이 더 좋을 것 같아서 정렬 후 이분 탐색을 진행한다.
(참고로 max와, min함수의 시간 복잡도는 O(n)이고 sort함수의 시간 복잡도는 O(n*logn)이고, 실제 백준 채점기로는 두 방법 모두 실행시간이 동일하다!)
2. 이분 탐색을 시작한다.
2 - 1) 현재 mid값은 테스트 케이스 1을 기준으로 401이라는 값을 갖게 된다.
2 - 2) 만약 mid값이 0이라는 뜻은 high와 low가 둘 다 0일 때이다. 문제에서 기존의 K개의 랜선으로 N개의 랜선을 못 만드는 경우는 없다고 했기 때문에 1을 리턴하면 된다. (1cm 간격으로 다 잘라야 N개가 만들어진다는 뜻이다)
2 - 3) 정렬이 된 리스트의 원소를 하나씩 순회하면서 값의 몫을 카운트한다.
* 나머지는 버리고 몫만 세는 이유는 문제의 조건에서 자르고 남은 랜선은 사용이 불가능하다고 했기 때문이다. 테스트 케이스를 대입했다면, 리스트의 두 번째 값은 743인데, 401로 나누면 몫은 1, 나머지는 342가 된다.
2 - 4) 만약 cnt 변수가 이미 N과 같거나 이미 초과했다면, result 변수에 현재 mid값을 대입하고 반복문을 빠져나온다.
*N개보다 많이 만드는 것도 허용한다는 문제의 조건이 있다.
2 - 5) 만약 cnt 값이 n보다 작다면 mid를 기준으로 더 아래에 있는 값을 기준으로 탐색을 다시 시작하고, 반대의 경우라면 더 위에 있는 값을 기준으로 탐색을 다시 시작한다.
2 - 6) 최종적으로 나온 result는 최댓값이 나와야 하기 때문에 중간에 "cnt == n"조건을 만족하는 mid를 찾았더라도 끝까지 탐색을 해야 한다.
3. 이분 탐색으로 나온 결과를 출력한다.

max함수를 사용할 때와 정렬된 리스트를 사용한 경우 차이가 없었다는 것도 확인할 겸 두 개의 결과를 나란히 찍어봤다.
블로그를 운영한 지 얼마 되지 않아서 나만의 프레임이 없다.
매번 새로운 프레임으로 예쁘게 정리해보려고 노력 중이다.
'프로그래밍 > Algorithm' 카테고리의 다른 글
| [백준] 2217번 로프 파이썬 해설 (0) | 2019.09.29 |
|---|---|
| [백준] 2178번 미로 탐색 파이썬 해설 (0) | 2019.09.26 |
| [백준] 1904번 01타일 파이썬 해설 (1) | 2019.09.24 |
| [백준] 2579번 계단오르기 파이썬 해설 (2) | 2019.09.13 |


댓글